2024-12-05
<2024-12-05 Thu>
(kevin-kelly-68.t2t) Following your bliss is a recipe for paralysis if you don’t know what you are passionate about. A better motto for most youth is “master something, anything”. Through mastery of one thing, you can drift towards extensions of that mastery that bring you more joy, and eventually discover where your bliss is.
어떤 것에 열정을 가지고 있는지 모른 체 단순히 행복만을 좇다␜보면 무기력해지게 됩니다. 많은 젊은이들을 위한 좀 더 좋은 모토는 "뭔가를 마스터하세요. 어떤것이라도" 입니다. 한 가지 숙달하는 것을 통해서 더 큰 기쁨을 주는 다른 것으로 확장해 갈 수 있고, 결국엔 행복이 어디에 있는지 알게 됩니다.
- [ ] #모닝페이지
- [ ] #딥워크
- [ ] #가족 #정리
- [ ] #요약
14:38 호매실도서관 불타게 달리는 중. 잠시만, 오전에 알게 된 것. 미분기하학 - 수식 이야기
잠시만, 핵심 개념을 다루는데 노트는 밀리기 매우 쉽다. 무엇을 어떻게 정리할것인가?
DONE 14:43 #브레인워시
아 졸려. 피곤하다 잠시만 휴식하자.
15:28 맹세 각서 통제 조건
약속 각서 맹세 강제
채식주의
16:15 관계 라는 단어의 역할
TODO #수학 mathematics, math, maths
(“수학 Mathematics, Math, Maths” 2024)
수학(數學, 영어: mathematics, math, maths)은 수, 양, 구조, 공간, 변화 등의 개념을 다루는 학문이다. 널리 받아들여지는 명확한 정의는 없으나 현대 수학은 일반적으로 엄밀한 논리에 근거하여 추상적 대상을 탐구하며, 이는 규칙의 발견과 문제의 제시 및 해결의 과정으로 이루어진다. 수학은 그 발전 과정에 있어서 철학, 과학과 깊은 연관을 맺고 있으며, 엄밀한 논리와 특유의 추상성, 보편성에 의해 다른 학문들과 구별된다. 특히 수학은 과학의 여느 분야들과는 달리 자연계에서 관측되지 않는 개념들에 대해서까지 이론을 추상화시키는 특징을 보이는데, 수학자들은 그러한 개념들에 대한 추측을 제시하고 적절하게 선택된 정의와 공리로부터 엄밀한 연역을 거쳐 그 진위를 파악한다. 수학의 개념들은 기원전 600년 경에 활동하며 최초의 수학자로도 여겨지는 탈레스의 기록은 물론, 다른 고대 문명들에서도 찾아볼 수 있으며 인류의 문명과 함께 발전해 왔다. 오늘날 수학은 자연과학, 사회과학, 공학, 의학 등 거의 모든 학문에서도 핵심적인 역할을 하며 다양한 방식으로 응용된다. 수학을 의미하는 mathematics라는 단어는 ’아는 모든 것’, ’배우는 모든 것’이라는 뜻의 고대 그리스어 ’máthēma’(μάθημα) 및 그 활용형 mathēmatikós(μαθηματικός)에서 유래되었다.
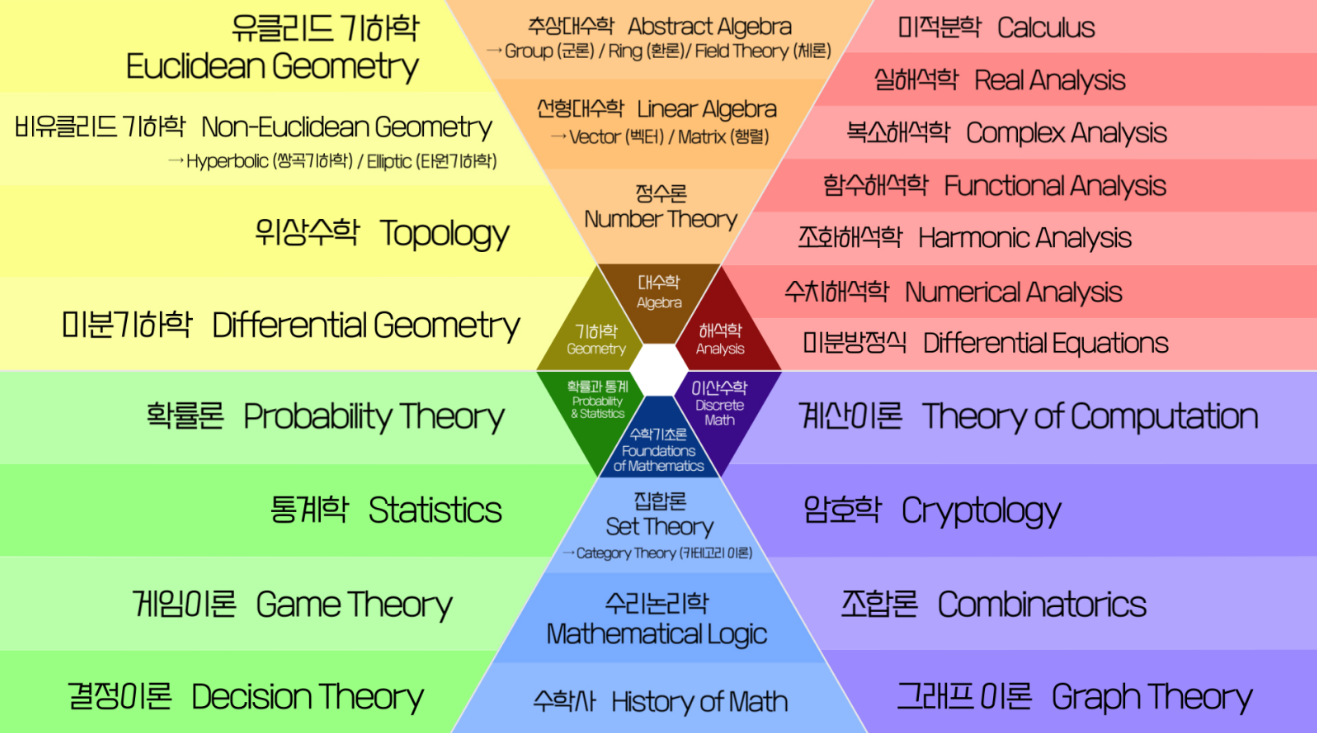 >
>
수학의 분류 (다양한 스펙트럼) | 매스프레소 - youtube.com
TODO 미분기하학 differential geometry
(“미분기하학 Differential Geometry” 2024)
- 미분기하학(微分幾何學, differential geometry)은 기하학의 문제를 다루기 위해 미적분, 해석학, 선형대수학, 그리고 다중선형대수학을 이용한 수학의 한 분야이다. 3차원 유클리드 공간에서의 평면, 곡면 그리고 곡선에 대한 이론들이 18세기와 19세기 동안 미분 기하학의 발전의 기초가 되었다. 19세기 후반부터, 미분 기하학은 매끄러운 다양체의 기하적 구조를 조금 더 일반적으로 다루는 한 분야로 성장했다. 미분 기하학은 미분위상수학과 긴밀히 연결되어 있고 기하학의 관점으로 볼때 미분 방정식과도 관련이 있다. 리치 흐름(Ricci flow)을 이용한 푸앵카레 추측에 대한 그리고리 페렐만의 증명은 위상 수학 문제의 접근에서 미분 기하학적 툴의 강력함을 보여주었으며 해석적 방법이 중요하다는 것을 다시 한 번 보여주었다. 특히, 곡면에 대한 미분 기하학은 미분 기하학의 특성에 대해 많은 이해와 기법의 단초를 제공한다.
키워드
분야(branches)
• 유클리드 • 비유클리드 • 타원 • 구면 • 쌍곡 • 비아르키메데스(non-Archimedean) • 사영 • 아핀 • 종합(synthetic) • 해석 • 대수
• 산술(arithmetic) • 디오판토스
• 미분
• 리만 • 심플레틱(symplectic) • 이산 미분(discrete differential)
• 복소 • 유한(finite) • 이산/결합(ciscrete/ccmbinatorial)
• 볼록(convex) • 계산 • 프랙탈 • 발생(incidence) • 비가환 기하학
• 비가환 대수(Noncommutative algebraic)
개념 특징
차원
• 컴퍼스와 자 작도 • 각도 • 곡선 • 대각선 • 직교 (수직선) • 평행 • 꼭짓점 • 합동 • 닮음 • 대칭
0차원 • 점
1차원
2차원
삼각형
• 높이(altitude) • 빗변 • 피타고라스 정리
평행사변형
• 정사각형 • 직사각형 • 마름모 • 편능형(Rhomboid)
사각형
원
3차원
• 부피 • 정육면체 • cuboid • 원기둥 • 십이면체 • 이십면체 • 팔면체 • 각뿔 • 정다면체 • 구 • 사면체
4차원- / 다른 차원
기하학자
이름별
• 아이다 • 아리아바타 • 아메스 • 알하이삼 • 아폴로니오스 • 아르키메데스 • 아티야 • 보드하야나(Baudhayana) • 보여이 • 브라흐마굽타(Brahmagupta) • 카르탕 • 콕서터 • 데카르트 • 유클리드 • 오일러 • 가우스 • 그로모프 • 힐베르트 • 제하데바 • 카티야나(Kātyāyana) • 하이얌 • 클라인 • 로바쳅스키 • 마나바(Manava) • 민코프스키 • 명안도 • 파스칼 • 피타고라스 • Parameshvara(파라메쉬바라) • 푸앵카레 • 리만 • 사카베(Sakabe) • 시찌(Sijzi) • 알투시 • 베블런 • 비라세나(Virasena) • 양휘 • 알-야사민(al-Yasamin) • 장형 • 기하학자 목록(List of geometers)
시대별
기원전(BCE)
• 아메스 • 보드하야나(Baudhayana) • 마나바(Manava) • 피타고라스 • 유클리드 • 아르키메데스 • 아폴로니오스
1–1400년대
• 장형 • 카티야나(Kātyāyana) • 아리아바타 • 브라흐마굽타(Brahmagupta) • 비라세나(Virasena) • 알하이삼 • 시찌(Sijzi) • 하이얌 • 알-야사민(al-Yasamin) • 알투시 • 양휘 • Parameshvara(파라메쉬바라)
1400년대–1700년대
• 제하데바 • 데카르트 • 파스칼 • 명안도 • 오일러 • 사카베(Sakabe) • 아이다
1700년대–1900년대
• 가우스 • 로바쳅스키 • 보여이 • 리만 • 클라인 • 푸앵카레 • 힐베르트 • 민코프스키 • 카르탕 • 베블런 • 콕서터
현재
미분기하학
말안장처럼 생긴 곡면 (쌍곡포물면(hyperbolic parabloid))위의 삼각형과 발산하는 평행선 학문명 미분기하학
미분기하학(微分幾何學, differential geometry)은 기하학의 문제를 다루기 위해 미적분, 해석학, 선형대수학, 그리고 다중선형대수학을 이용한 수학의 한 분야이다. 3차원 유클리드 공간에서의 평면, 곡면 그리고 곡선에 대한 이론들이 18세기와 19세기 동안 미분 기하학의 발전의 기초가 되었다. 19세기 후반부터, 미분 기하학은 매끄러운 다양체의 기하적 구조를 조금 더 일반적으로 다루는 한 분야로 성장했다. 미분 기하학은 미분위상수학과 긴밀히 연결되어 있고 기하학의 관점으로 볼때 미분 방정식과도 관련이 있다. 리치 흐름(Ricci flow)을 이용한 푸앵카레 추측에 대한 그리고리 페렐만의 증명은 위상 수학 문제의 접근에서 미분 기하학적 툴의 강력함을 보여주었으며 해석적 방법이 중요하다는 것을 다시 한 번 보여주었다. 특히, 곡면에 대한 미분 기하학은 미분 기하학의 특성에 대해 많은 이해와 기법의 단초를 제공한다.
하부 분야
[편집]
리만 기하학
리만 기하학은 계량 텐서가 주어진 리만 다양체와 매끄러운 다양체에 대해 연구한다. 리만 계량 텐서는 매끄러운 양의 정부호 대칭 이중선형꼴로 각 점에서의 접평면에서 정의되는 거리에 대한 개념이다. 리만 기하학은 각 점에서 "미소"하게, 즉, 1차 근사로, 유클리드 공간으로 여길수 있지만 실제로 공간이 평평할 필요가 없는 공간에서 유클리드 기하를 일반화시켰다. 곡선의 길이, 면의 넓이, 입체의 부피 같은 길이에 대한 다양한 개념들을 리만 기하학에서 모두 자연스럽게 유추할 수 있다. 다변수 미적분학에서 함수의 방향 도함수의 개념이 리만 기하학에서는 텐서의 공변 미분으로 확장되었다. 해석학과 미분방정식의 많은 개념과 기법들이 리만 다양체를 정의하여 일반화되었다.
리만 다양체 사이에 거리를 보존하는 미분동형사상은 등거리변환이라 부른다. 이 개념 또한 국소적(즉, 한 점의 좁은 근방)으로 정의될 수 있다. 어느 두 표준 곡선은 지역적으로 등거리 변환이다. 하지만 이미 가우스의 빼어난 정리는 표면에서 지역적 등거리변환의 존재성이 강한 양립가능성을 의미한다는 것을 보여주었다. 즉, 대응되는 점들의 가우스 곡률은 반드시 같아야 한다. 고차원에서 리만 곡률 텐서는 리만 다양체와 관련된 얼마나 평평한지를 측정해주는 각 점을 기준으로 한 좋은 불변량이다. 리만 다양체의 중요한 류(class)는 리만 대칭 공간이다. 리만 대칭 공간의 곡률은 꼭 일정할 필요가 없다. 이들은 유클리드 기하와 비유클리드 기하에서의 "보통의" 평면과 공간에서 가장 근접한 유추이다.
준 리만 기하학
[편집]
준 리만 기하학(영어: pseudo-Riemannian geometry)은 계량 텐서가 양의 정부호일 필요가 없는 경우의 리만 기하학을 일반화시킨 것이다. 로런츠 다양체는 준 리만 기하학의 특수한 경우이다. 로렌츠 다양체는 일반 상대성 이론의 수학적 토대를 이룬다.
심플렉틱 기하학
[편집] ,* 이 부분의 본문은 심플렉틱 다양체입니다.
기하 해석학
[편집]
(비)선형 편미분 방정식을 이용하여 미분 위상수학과 미분 기하학의 결과들을 얻는 분야이다. 극소 곡면에 관한 이론, 호지 이론 등등이 기하 해석학의 결과들이다. 푸엥카레의 추측이 기하 해석학의 주요 문제 중 하나이다.
스펙트랄 기하학
[편집]
핀슬러 기하학
관련된 수학
[편집]
복소 기하학
미분 위상 수학
리군
리 군(Lie group)은 군(group)이면서 매끄러운 다양체다. 기하학적 대칭들로 이뤄진 군들은 리 군인 경우가 많다. 대표적으로, 평면 상에서 회전군 U(1), 3차원 유클리드공간 상에서 회전군 SO(3)가 있다. 또한 여러 가지 중요한 행렬군들인 일반선형군 GL(n), 유니터리 군 U(n), 특수 유니터리 군 SU(n), 직교군 O(n) 등도 리 군이다.
다발과 접속
내적 성질과 외적 성질
[편집]
18세기 초중반부터 미분기하는 외적 관점으로 연구되었다. 곡선과 곡면은 고차원 유클리드 공간 내에 있는 것으로 생각했었다 (예를 들면 곡면은 곡면의 주변 공간인 3차원 내의 공간으로 볼 수 있다). 베른하르트 리만의 연구로부터 내적 관점에서의 연구가 발전되기 시작했다. 내적 관점의 연구는 기하학적 대상 그 자체를 독립적으로 생각하기 때문에 기하학적 대상 밖으로 움직인다고 말할 수 없다. 내적 관점으로부터 만들어진 기초적인 결과중 하나는 가우스의 빼어난 정리이다. 가우스의 빼어난 정리는 가우스 곡률은 내적 불변량이라는 의미를 가진다. 내적 관점이 응용에 있어 더 유용할 때도 있다. 예를 들면 상대성이론에서 내적 관점은 유용하다. 시공간이 외적으로 생각하는 게 자연스러울 수가 없기 때문이다. (시공간 "밖"의 것은 무언가를 생각해보라.) 내적 관점에서는 곡률의 핵심적 개념과 아핀 접속과 같은 다른 개념들은 정의하기가 더 어렵다. 그러므로 각각의 관점마다 장점이 있다. 하지만, 이 기하학적 대상에 대한 두 가지 관점을 조화시킬 수 있다. 즉, 외적 관점의 기하학은 내적 관점의 기하학에 더한 어떤 구조로 생각할 수 있다.
응용
[편집]
미분기하학은 수학 밖에서 폭넓게 응용된다.
이론 물리학은 미분기하학을 광범위하게 사용한다. 고전역학에서는 라그랑주 역학은 짜임새 공간의 접다발 위에서 정의되며, 해밀턴 역학은 짜임새 공간의 여접다발(위상 공간) 또는 보다 일반적으로 임의의 심플렉틱 다양체 위에 정의된다. 전자기학과 양-밀스 이론, 나아가 표준 모형은 시공간 위에 정의되는 주다발의 주접속과 곡률을 다룬다. 중력을 다루는 이론인 일반 상대성 이론은 유사 리만 다양체의 리치 곡률을 다룬다. 또한, 끈 이론에서는 칼라비-야우 다양체, 켈러 다양체와 초켈러 다양체 등 수많은 미분기하학적 개념들이 필수적이다.
딥러닝, 컴퓨터 비전에서는, 이미지를 처리할 때 미분기하학을 쓴다.
같이 보기
[편집]
• 비가환 기하학 • 수축량 • 게이지 이론 (수학)
참고 문헌
[편집] ,* 위키미디어 공용에 관련된 미디어 분류가 있습니다. 미분기하학
• 김강태 (2000). 《미분기하학》. 교우사. ISBN 978-898172226-5. • 윤갑진 (2007). 《미분기하학》 개정판. 경문사. ISBN 978-89-6105-045-6.[깨진 링크 (과거 내용 찾기)] • 최대호 (2007). 《미분기하학》 3판. 경문사. ISBN 89-7282-000-8.[깨진 링크(과거 내용 찾기)] • 박진석; 표용수; 김향숙 (2011). 《Mathematica를 활용한 미분기하학 개론》 8판. 경문사. ISBN 978-89-6105-424-9.[깨진 링크(과거 내용 찾기)] • Pressley, Andrew N. (2012). 《Elementary differential geometry》. Springer Undergraduate Mathematics Series (영어) 2판. Springer. doi:10.1007/978-1-84882-891-9. ISBN 978-1-84882-890-2. ISSN 1615-2085. • Gadea, Pedro M.; Muñoz Masqué, Jaime; Mykytyuk, Ihor V. (2013). 《Analysis and algebra on differentiable manifolds: a workbook for students and teachers》. Problem Books in Mathematics (영어) 2판. Springer. doi:10.1007/978-94-007-5952-7. ISBN 978-94-007-5951-0. ISSN 0941-3502. • Lange, Serge (1999). 《Fundamentals of differential geometry》. Graduate Texts in Mathematics (영어) 191. Springer-Verlag. doi:10.1007/978-1-4612-0541-8. ISBN 978-0-387-98593-0. ISSN 0072-5285. • Chern, Shiing-Shen; Chen, Wei-Huan; Lam, Kai-Shue (1999년 11월). 《Lectures on differential geometry》. Series on University Mathematics (영어) 1. World Scientific. doi:10.1142/3812. ISBN 978-981-02-3494-2. • McCleary, John (2012년 11월). 《Geometry from a differentiable viewpoint》 (영어) 2판. Cambridge University Press. doi:10.1017/CBO9781139022248. ISBN 978-052113311-1. • Lafontaine, Jacques (2010). 《Introduction aux variétés différentielles》 (프랑스어). Édition Diffusion Presse Sciences. ISBN 978-2-7598-0572-3.[깨진 링크 (과거 내용 찾기)]
외부 링크
• 김영욱. “미분기하 공부하기” (PDF). 2012년 11월 1일에 원본 문서 (PDF)에서 보존된 문서. 2013년 8월 21일에 확인함.
미분기하학 - 나무위키
https://namu.wiki/w/%EB%AF%B8%EB%B6%84%EA%B8%B0%ED%95%98%ED%95%99
TODO 미적분학의 본질 | 3b1b 한국어
(3b1b n.d.)
- 3b1b
- 3Blue1Brown의 대표 시리즈 "Essence of Calculus"의 한국어 번역. 여러분이 직접 미적분학을 발명할 수도 있었다는 느낌을 심어주는 것이 영상의 목표입니다.
https://youtube.com/playlist?list=PLkoaXOTFHiqjfsanyvicarnZv-YLC8QN-&si=fDx6zDbV6_7nRjFD
DONE #clj-tiles: #STEM #비주얼프로그래밍
DONE 테마 변경 내용
DONE From 맹세 각서 통제 조건허락 to 조건 집착 없이 내맡기는삶
Related-Notes
- dd
References
3b1b. n.d. “미적분학의 본질 | 3b1b 한국어.” YouTube. Accessed November 17, 2024. http://www.youtube.com/playlist?list=PLkoaXOTFHiqjfsanyvicarnZv-YLC8QN-.
“미분기하학 Differential Geometry.” 2024. In 위키백과, 우리 모두의 백과사전. https://ko.wikipedia.org/w/index.php?title=%EB%AF%B8%EB%B6%84%EA%B8%B0%ED%95%98%ED%95%99&oldid=37354097.
“수학 Mathematics, Math, Maths.” 2024. In 위키백과, 우리 모두의 백과사전. https://ko.wikipedia.org/w/index.php?title=%EC%88%98%ED%95%99&oldid=37803756.